配景

在物聯網、監控、傳感器、金融等應用領域,數據在時間維度上流式的產生,并且數據量非常龐大.

例如我們經常看到的性能監控視圖,便是很多點在時間維度上描繪的曲線.

又好比金融行業的走勢數據等等.

我們想象一下,如果每個傳感器或指標每100毫秒產生1個點,一天便是864000個點.

而傳感器或指標是非常多的,例如有100萬個傳感器或指標,一天的量就接近一億的量.

假設我們要描繪一個時間段的圖形,這么多的點,渲染估計都要很久.

那么有沒有好的壓縮算法,即能保證失真度,又能很好的對數據進行壓縮呢?

旋轉門壓縮算法原理

旋轉門壓縮算法(SDT)是一種直線趨勢化壓縮算法,其本色是通過一條由起點和終點確定的直線代替一系列連續數據點.

該算法必要記錄每段時間間隔長度、起點數據和終點數據, 前一段的終點數據即為下一段的起點數據.

其基來源根基理較為簡單, 參見圖.

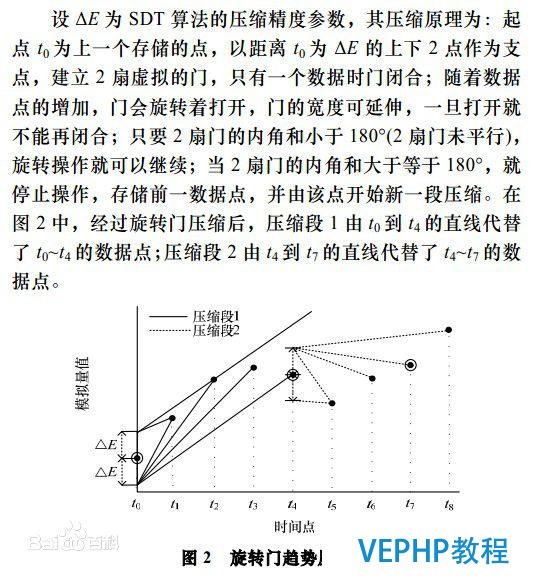
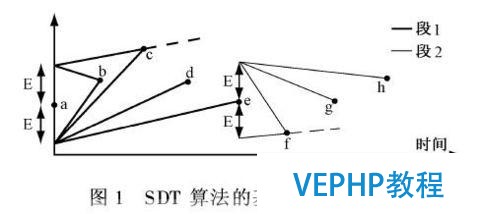
第一個數據點a上下各有一點,它們與a點之間的距離為E(即門的寬度), 這兩個點作為“門”的兩個支點.

當只有第一個數據點時,兩扇門都是關閉的;隨著點數越來越多,門將逐步打開;注意到每扇門的寬度是可以伸縮的,在一段時間間隔里面,門一旦打開就不克不及閉;

只要兩扇門未達到平行,或者說兩個內角之和小于180°(本文的算法將利用這一點進行判斷),這種“轉門”操作即可繼續進行.

圖中第一個時間段是從a到e, 成果是用a點到e點之間的直線代替數據點(a,b,c,d,e); 起到了可控失真(E)的壓縮作用.

第二個時間間隔從e點開始,開始時兩扇門關閉,然后逐步打開,后續操作與前一段類似.

在PostgreSQL中實現旋轉門壓縮算法

通過旋轉門算法的原理,可以了解到,有幾個需要的輸入項.

• 有x坐標和y坐標的點(如果是時間軸上的點,可以通過epoch轉換成這種形式)

• E,即門的寬度,起到了控制壓縮失真度的作用

例子

創立測試表

create table tbl(id int, -- ID,可有可無val numeric, -- 值(如傳感器或金融行業的點值)t timestamp -- 取值時間戳);

插入10萬條測試數據

insert into tbl select generate_series(1,100000), round((random()*100)::numeric, 2), clock_timestamp()+(generate_series(1,100000) || ' second')::interval ; test=> select * from tbl limit 10;

id | val | t

----+-------+----------------------------

1 | 31.79 | 2016-08-12 23:22:27.530318

2 | 18.23 | 2016-08-12 23:22:28.530443

3 | 5.14 | 2016-08-12 23:22:29.530453

4 | 90.25 | 2016-08-12 23:22:30.530459

5 | 8.17 | 2016-08-12 23:22:31.530465

6 | 97.43 | 2016-08-12 23:22:32.53047

7 | 17.41 | 2016-08-12 23:22:33.530476

8 | 0.23 | 2016-08-12 23:22:34.530481

9 | 84.67 | 2016-08-12 23:22:35.530487

10 | 16.37 | 2016-08-12 23:22:36.530493

(10 rows)

時間如何轉換成X軸的數值,假設每1秒為X坐標的1個單位

test=> select (extract(epoch from t)-extract(epoch from first_value(t) over())) / 1 as x, -- 除以1秒為1個單位

val, t from tbl limit 100;

x | val | t

------------------+-------+----------------------------

0 | 31.79 | 2016-08-12 23:22:27.530318 1.00012493133545 | 18.23 | 2016-08-12 23:22:28.530443 2.00013494491577 | 5.14 | 2016-08-12 23:22:29.530453 3.00014090538025 | 90.25 | 2016-08-12 23:22:30.530459 4.00014686584473 | 8.17 | 2016-08-12 23:22:31.530465 5.00015187263489 | 97.43 | 2016-08-12 23:22:32.53047 6.00015807151794 | 17.41 | 2016-08-12 23:22:33.530476 7.00016307830811 | 0.23 | 2016-08-12 23:22:34.530481 8.00016903877258 | 84.67 | 2016-08-12 23:22:35.530487

編寫實現螺旋門算法的函數

create or replace function f (

i_radius numeric, -- 壓縮半徑

i_time timestamp, -- 開始時間

i_interval_s numeric, -- 時間轉換間隔 (秒,例如每5秒在坐標上表現1個單位間隔,則這里使用5)

query text, -- 需要進行旋轉門壓縮的數據, 例子 'select t, val from tbl where t>=%L order by t limit 100' , select 子句必需固定, 必需按t排序

OUT o_val numeric, -- 值,縱坐標 y (跳躍點y)

OUT o_time timestamp, -- 時間,橫坐標 x (跳躍點x)

OUT o_x numeric -- 跳躍點x, 通過 o_time 轉換)

returns setof record as $$

declare

v_time timestamp; -- 時間變量

v_x numeric; -- v_time 轉換為v_x

v_val numeric; -- y坐標

v1_time timestamp; -- 前一點 時間變量

v1_x numeric; -- 前一點 v_time 轉換為v_x

v1_val numeric; -- 前一點 y坐標

v_start_time numeric; -- 記錄第一條的時間坐標, 用于計算x偏移量

v_rownum int8 := 0; -- 用于標志是否第一行

v_max_angle1 numeric; -- 最大上門夾角角度

v_max_angle2 numeric; -- 最大下門夾角角度

v_angle1 numeric; -- 上門夾角角度

v_angle2 numeric; -- 下門夾角角度begin

for v_time , v_val in execute format(query, i_time)

LOOP

-- 第一行,第一個點,是實際要記錄的點位

v_rownum := v_rownum + 1; if v_rownum=1 then

v_start_time := extract(epoch from v_time);

v_x := 0;

o_val := v_val;

o_time := v_time;

o_x := v_x;

-- raise notice 'rownum=1 %, %', o_val,o_time;

return next; -- 返回第一個點

else

v_x := (extract(epoch from v_time) - v_start_time) / i_interval_s; -- 生成X坐標

SELECT 180-ST_Azimuth(

ST_MakePoint(o_x, o_val+i_radius), -- 門上點

ST_MakePoint(v_x, v_val) -- next point

)/(2*pi())*360 as degAz, -- 上夾角

ST_Azimuth(

ST_MakePoint(o_x, o_val-i_radius), -- 門下點

ST_MakePoint(v_x, v_val) -- next point

)/(2*pi())*360 As degAzrev -- 下夾角

INTO v_angle1, v_angle2;

select GREATEST(v_angle1, v_max_angle1), GREATEST(v_angle2, v_max_angle2) into v_max_angle1, v_max_angle2; if (v_max_angle1 + v_max_angle2) >= 180 then -- 找到四邊形外的點位,輸出上一個點,并從上一個點開始重新計算四邊形

-- raise notice 'max1 %, max2 %', v_max_angle1 , v_max_angle2;

-- 復原

v_angle1 := 0;

v_max_angle1 := 0;

v_angle2 := 0;

v_max_angle2 := 0; -- 門已完全打開,輸出前一個點的值

o_val := v1_val;

o_time := v1_time;

v1_x := (extract(epoch from v1_time) - v_start_time) / i_interval_s; -- 生成前一個點的X坐標

o_x := v1_x;

-- 用新的門,與當前點計算新的夾角

SELECT 180-ST_Azimuth(

ST_MakePoint(o_x, o_val+i_radius), -- 門上點

ST_MakePoint(v_x, v_val) -- next point

)/(2*pi())*360 as degAz, -- 上夾角

ST_Azimuth(

ST_MakePoint(o_x, o_val-i_radius), -- 門下點

ST_MakePoint(v_x, v_val) -- next point

)/(2*pi())*360 As degAzrev -- 下夾角

INTO v_angle1, v_angle2; select GREATEST(v_angle1, v_max_angle1), GREATEST(v_angle2, v_max_angle2) into v_max_angle1, v_max_angle2;

-- raise notice 'new max %, new max %', v_max_angle1 , v_max_angle2;

-- raise notice 'rownum<>1 %, %', o_val, o_time;

return next; end if;

-- 記錄當前值,保留作為下一個點的前點

v1_val := v_val;

v1_time := v_time;

end if;

END LOOP;

end;

$$ language plpgsql strict;

壓縮測試

門寬為15,起始時間為'2016-08-12 23:22:27.530318',每1秒表現1個X坐標單位.

test=>

select * from f (

15, -- 門寬度=15

'2016-08-12 23:22:27.530318', -- 開始時間

1, -- 時間坐標換算間隔,1秒

'select t, val from tbl where t>=%L order by t limit 100' -- query

);

o_val | o_time | o_x

-------+----------------------------+------------------

18.23 | 2016-08-12 23:22:28.530443 | 0

5.14 | 2016-08-12 23:22:29.530453 | 1.00001287460327

90.25 | 2016-08-12 23:22:30.530459 | 2.00001883506775

......

87.90 | 2016-08-12 23:24:01.53098 | 93.0005400180817

29.94 | 2016-08-12 23:24:02.530985 | 94.0005450248718

63.53 | 2016-08-12 23:24:03.53099 | 95.0005497932434

12.25 | 2016-08-12 23:24:04.530996 | 96.0005559921265

83.21 | 2016-08-12 23:24:05.531001 | 97.0005609989166

(71 rows)

可以看到100個點,壓縮成了71個點.

對比一下本來的100個點的值

test=> select val, t, (extract(epoch from t)-extract(epoch from first_value(t) over()))/1 as x from tbl where t>'2016-08-12 23:22:27.530318' order by t limit 100;

val | t | x

-------+----------------------------+------------------

18.23 | 2016-08-12 23:22:28.530443 | 0

5.14 | 2016-08-12 23:22:29.530453 | 1.00001001358032

90.25 | 2016-08-12 23:22:30.530459 | 2.0000159740448

......

83.21 | 2016-08-12 23:24:05.531001 | 97.0005581378937

87.97 | 2016-08-12 23:24:06.531006 | 98.0005631446838

58.97 | 2016-08-12 23:24:07.531012 | 99.0005691051483

(100 rows)

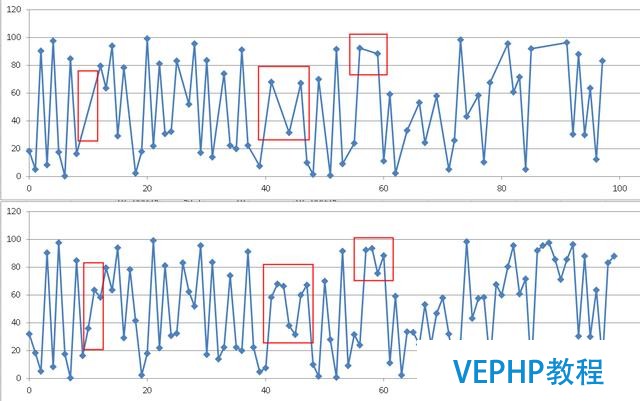
使用excel繪圖,進行壓縮前后的對比

上面是壓縮后的數據繪圖,下面是壓縮前的數據繪圖

紅色標記的位置,便是通過旋轉門算法壓縮掉的數據.

失真度是可控的.

流式壓縮的實現

本文略,其實也很簡單,這個函數改一下,創立一個以數組為輸入參數的函數.

以lambda的方式,實時的從流式輸入的管道取數,并執行即可.

也可以寫成聚合函數,在基于PostgreSQL 的流式數據庫pipelineDB中調用,實現流式計算.

http://www.pipelinedb.com/

小結

通過旋轉門算法,對IT監控、金融、電力、水利等監控、物聯網、等流式數據進行實時的壓縮.

數據不必要從數據庫LOAD出來即可在庫內完成運算和壓縮.

用戶也可以根據實際的需求,進行流式的數據壓縮,同樣數據也不必要從數據庫LOAD出來,在數據庫端即可完成.

PostgreSQL的功能一如既往的強大,好用,快用起來吧.

參考

1. http://baike.baidu.com/view/3478397.htm

2. http://postgis.net/docs/manual-2.2/ST_Azimuth.html

3. https://www.postgresql.org/docs/devel/static/functions-conditional.html

4. http://gis.stackexchange.com/questions/25126/how-to-calculate-the-angle-at-which-two-lines-intersect-in-postgis

5. http://gis.stackexchange.com/questions/668/how-can-i-calculate-the-bearing-between-two-points-in-postgis

6. http://www.pipelinedb.com/

更多深度技術內容,請存眷云棲社區微信公眾號：yunqiinsight.